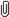Αποσπασμα απο το βιβλιο μεταφορας θερμοτητας και μαζας που ειχα στο ΕΜΠ
***
Yπάρχει κάποια απλή σχέση που αποτελεί µια πρώτη προσέγγιση του προβλήµατος και σύµφωνα µε την οποία το ποσό θερµότητας dQ, το οποίο µεταφέρεται κατά µήκος φλέβας διατοµής S, σε χρόνο dt, µεταξύ δύο σηµείων µε διαφορά θερµοκρασίας ∆T, είναι:
dQ = h*S*∆T*dt ή dQ/dt=h*S*∆Τ => ΔΤ= (dQ/dt)/h*S (7.1)
όπου dQ/dt η θερµική ροή ή το θερµικό ρεύµα (**στη περιπτωση μας ειναι η θερμότητα ανα μοναδα χρονου που αποδιδεται απο το συρμα και που υπολογιζεται ευκολα απο την καταναλωμενη ισχυ που ειναι ολη θερμικη**).
O συντελεστής h ονοµάζεται συντελεστής θερµικής µεταφοράς και µετριέται σε cal/sec*cm2*grad.
H ανεπάρκεια της σχέσεως (7.1) καθίσταται αµέσως φανερή από το γεγονός ότι ο συντελεστής h εξαρτάται από πάρα πολλούς παράγοντες:
• Από τη γεωµετρία του χώρου, δηλαδή από τη σχετική θέση των επιφανειών µεταξύ των οποίων κινείται το ρευστό.
• Από την πυκνότητα, το ιξώδες, την ειδική θερµότητα του ρευστού.
• Από το είδος της ροής του ρευστού.
• Από τη διαφορά της θερµοκρασίας και τη θερµική ροή.
Eποµένως η σχέση 7.1 είναι στην πραγµατικότητα εµπειρική και γι’ αυτό η τιµή του συντελεστή h δίνεται από πίνακες. H ίδια σχέση µπορεί να χρησιµοποιηθεί και για την εξαναγκασµένη µεταφορά, όπου η µετακίνηση της µάζας οφείλεται σε εξωτερικό αίτιο, όπως αντλία, κυκλοφορητής ή ανεµιστήρας. Φυσικά τότε δεν είναι απαραίτητο το σηµείο µε την υψηλότερη θερµοκρασία να βρίσκεται χαµηλότερα, αλλά ο συντελεστής h δίνεται πάλι από πίνακες που, όµως, είναι διαφορετικοί για διαφορετικά εξωτερικά αίτια.
******
Επίσης εδω εχουμε και μεταφορα θερμότητα λόγω ακτινοβολίας αλλα ειναι σχετικα μικρη και δεν θα την λαβω υπόψην σε πρωτη φαση...
Δυστυχως δε βρηκα ακόμη πουθενα την h για γλυκερινη στη περιπτωση αντλίας (οπως το ρουφηγμα) ωστε να υπολογισω την θρμοκρασία που αναπτυσεται στα σημεια επαφης. Η θερμοκρασία αυτη πάντως σιγουρα φτανει σε μια θερμοκρασία κόντα την θερμοκρασία του συρματος όταν ΔΕΝ ρουφαμε και εαν φτασει τους 280 το ΑΕΡΙΟ VG θα μετατραπει σε προπανελη.
Τωρα την κανω διήμερο. Απο Δευτερα αμα βρω χρονο θα ξαναασχοληθω.
ΥΣ: Για να προλαβω διαφορους ενημερωνω ότι και τα αερια και τα υγρα ειναι ρευστα και οτι για να γινει ενας πιο σαφης υπολογισμος χρειαζεται εφαρμογη τρισδιατατων πεπερασμενων στοιχειων (η διπλωματικη μου στο ΕΜΠ ηταν η μοντελοποιήση κατακόρυφου απορροφητη Νερου-αμμωνιας με πεπερασμενα μια πιο απλη αναλογη διαδικασία μονο που εκει ηταν εριπου το αντιστροφο απο εδω).
Ο ανωτερω προσεγγιστικος υπολογισμός δεν είναι τρισδιαστατος και δεν λαμβανει υποψην του την μορφή της ροής (που ειναι τυρβωδης)
Στην πραγματικοτητα πρεπει να λυθει μια μερικη διαφορικη εξισωση ως προς x,y,z,t και όχι μονο ως προς t πραγμα που θελει πολυ χρονο και σιγουρα ειδικο προγραμμα πεπερασμενων
Οι θεωρίες της κατσαρολας που βραζει ΔΕΝ μας ενδιαφερουν εδω γιατι το αεριο VG μπορει να μετατραπει σε προπανελη και οχι μονο το υγρο και αρα δεν μας ενδιαφερουν τα περι θερμοκρασιων ατμοποιησης παρα μονο για την αλλαγη φασης (υγρο σε αεριο).


 37 Απαντήσεις
37 Απαντήσεις 18610 Εμφανίσεις
18610 Εμφανίσεις